Ako používať Fibonacciho úrovne na spôsob Joea DiNapoliho

Joe DiNapoli je uznávaný profesionálny obchodník s pôsobivými, vyše štyridsaťročnými obchodnými skúsenosťami. Upravil používanie Fibonacciho úrovní a vytvoril vlastný systém známy ako DiNapoliho metóda obchodovania. 

 

Zo všetkých dostupných Fibonacciho úrovní návratu - retracementu (.236, .382, .50, .618, .764) si J. DiNapoli vybral iba dve: .382 a .618. Všimol si totiž, že práve tieto úrovne fungujú pri retracemente ako významné úrovne podpory. Vykreslené sú na na grafe č. 1 nižšie. 

 

 

Graf č. 1. DiNapoliho úrovne retracementu 

 

 

 

Hlavná myšlienka DiNapoliho metódy je nasledovná: len čo cena odskočí od ktorejkoľvek z týchto úrovní a vytvorí vzor ABC, ide o indikáciu pokračovania trendu. 

 

 

Okrem spomínaných dvoch retracementových úrovní autor používa aj 3 úrovne rozšírenia (expanzie). Štvrtý, „super-rozšírený” objektívny bod, neskôr pridali ďalší obchodníci, ktorí používajú DiNapoli metódu. Tu sú tieto úrovne:

 

 

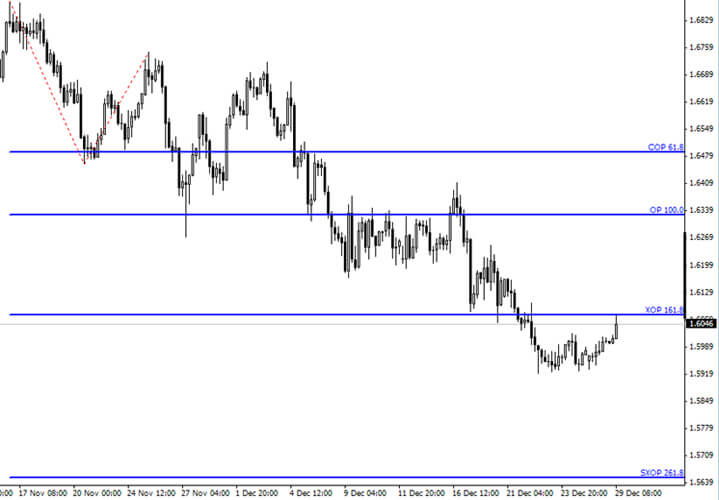
1. COP -  objektívny bod kontrakcie = 0,618 dĺžky vlny A meranej od konca korekčnej vlny B;

2. ОР - objektívny bod = 100 % dĺžky vlny A meranej od konca vlny B;

3. XOP - objektívny bod expanzie = 1,618 vlny A merané z B;

4. SXOP - objektívny bod super-expanzie = 2,618 vlny A merané z B.

 

 

Zjavným záverom pre aplikáciu týchto konkrétnych rozšírení je, že aj dĺžka korekčnej vlny zohráva významnú úlohu: všetky merania sa začínajú od konca korekčnej vlny B.

 

 

Začiatočníci často robia chybu v tom, že vypočítavajú úrovne expanzie (rozšírenia resp. predĺženia pohybu) a retracementu (návratu) vĺn, ktorých úloha a miesto im nie je celkom zrejmá. Joe DiNapoli tieto výpočty sprehladnil zavedením výrazu „reakčné číslo“, ktorý špecifikuje vlastné uzly (nody) Fibonacciho korekčných úrovní. Nasledujúca snímka obrazovky zobrazuje reakčné čísla reakcií a ich príslušné Fibonacciho rozšírenia (expanzie). Vďaka reakčným číslam budete vedieť, čo každý bod expanzie znamená a odkiaľ pochádza. Okrem toho môžete vidieť aj „spádové“ oblasti, do ktorých spadajú rozšírenia rôznych reakčných čísel, teda aspoň približne.

 

 

 

Posledná snímka obrazovky ukazuje všetky Fibonacciho návraty, rozšírenia a oblasti, kde sa pretínajú, pričom poskytujú silnú podporu a rezistenciu.